|
MAXIMA plot2d plot3d draw3d EXAMPLE
|
Maxima is a computer algebra system (CAS) based on a 1982 version of Macsyma.
License GPL
http://maxima.sourceforge.net/
https://wxmaxima-developers.github.io/wxmaxima/
Rosenbrock's valley, Funkcja Rosenbrocka, Dolina Rosenbrocka
Howard Harry Rosenbrock
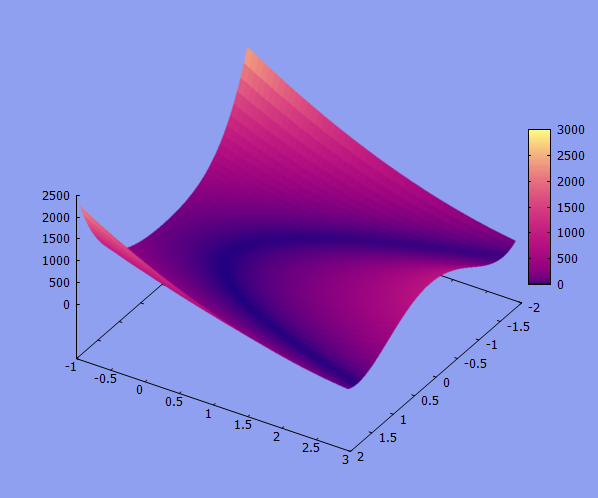
draw3d( enhanced3d=true, palette=[8,4,1], explicit((1-x)^2 + 100*(y-x^2)^2,x,-2,2,y,-1,3) );
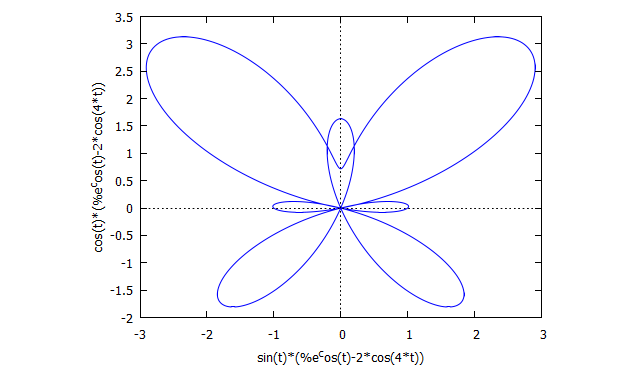
Butterfly curve (transcendental)
https://en.wikipedia.org/wiki/Parametric_equation
https://en.wikipedia.org/wiki/Butterfly_curve_(transcendental)
plot2d([parametric, sin(t)*(%e^(cos(t))-2*cos(4*t)), cos(t)*(%e^(cos(t))-2*cos(4*t)), [t,-10,10] ]);
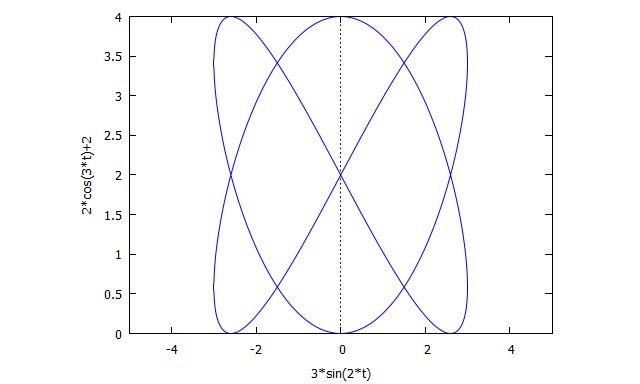
Lissajous curve, Lissajous figure, Krzywa Lissajous
plot2d( [ parametric,3*sin(2*t), 2+2*cos(3*t),[t,0,2*%pi] ], [x,-5,5] );
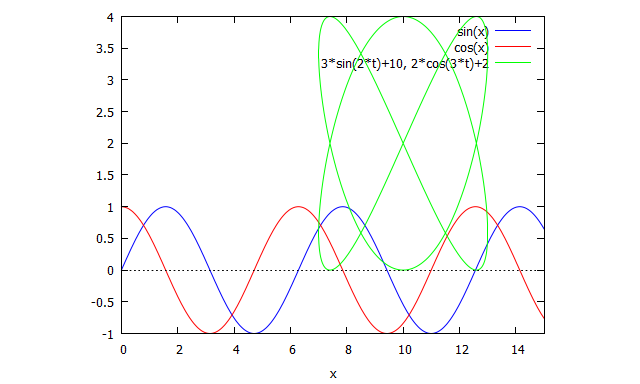
plot2d( [ sin(x), cos(x), [ parametric,10+3*sin(2*t), 2+2*cos(3*t),[t,0,2*%pi] ]], [x,0,15] );
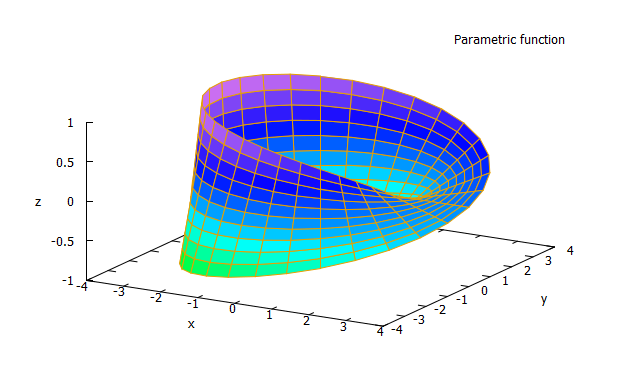
Mobius strip, Mobius loop, wstega Mobiusa
plot3d ([cos(x)*(3 + y*cos(x/2)), sin(x)*(3 + y*cos(x/2)), y*sin(x/2)], [x, -%pi, %pi], [y, -1, 1], [grid, 30, 10]);
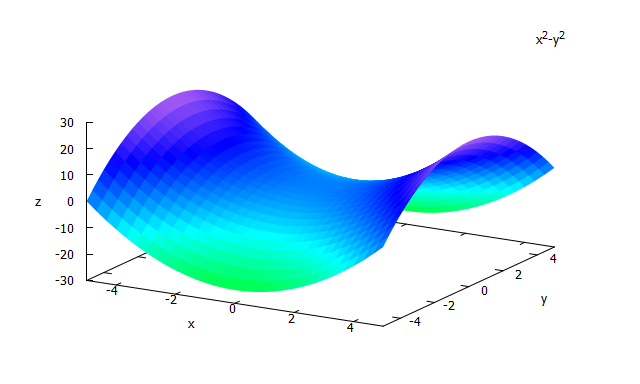
Hyperbolic paraboloid
plot3d(x^2 - y^2, [x, -5, 5], [y, -5, 5], [mesh_lines_color, false]);
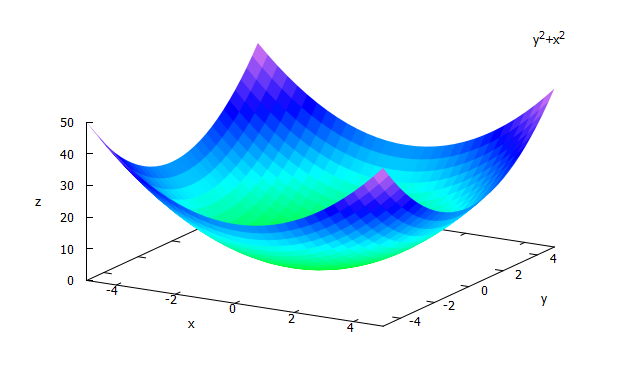
Elliptic Paraboloid
plot3d(x^2 + y^2, [x, -5, 5], [y, -5, 5], [mesh_lines_color, false]);
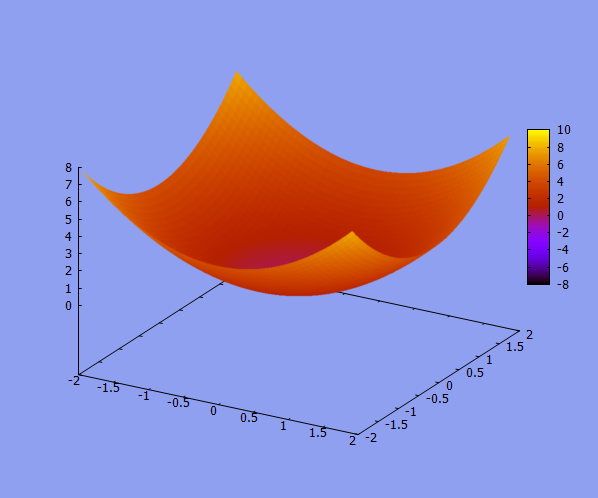
Elliptic Paraboloid
draw3d (enhanced3d = true, cbrange = [-8,10], explicit(x^2+y^2, x,-2,2,y,-2,2));
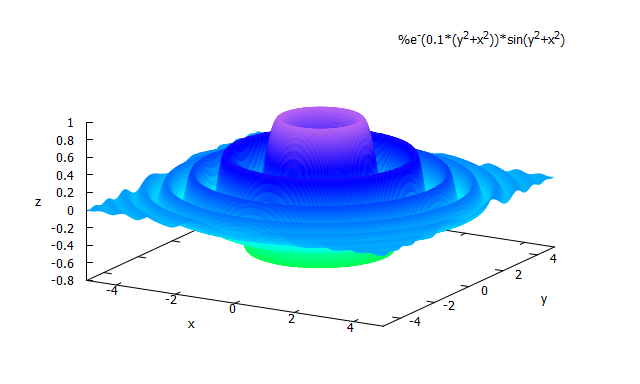
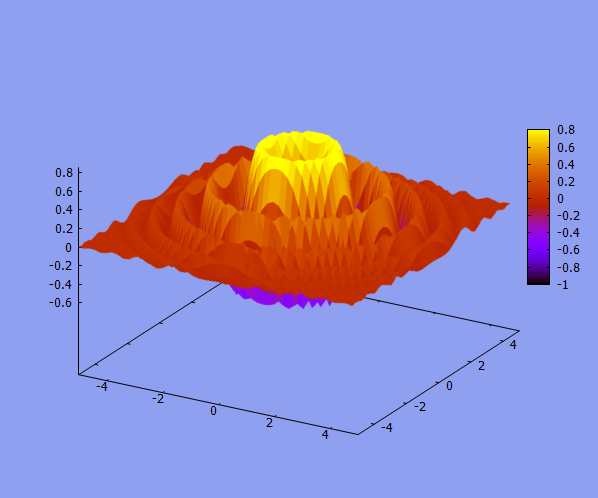
plot3d( sin(x^2+y^2)*exp(-0.1*(x^2+y^2) ), [x,-5,5],[y,-5,5],[grid,100,100], [mesh_lines_color, false] );
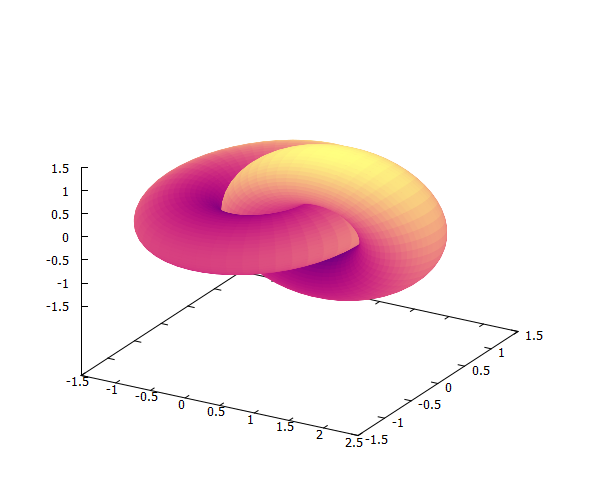
draw3d(enhanced3d = sin(u)+cos(v),terminal = wxt,colorbox=false,palette = [8,4,1],parametric_surface(cos(u)+.5*cos(u)*cos(v),sin(u)+.5*sin(u)*cos(v),.5*sin(v),u, -%pi, %pi,v, -%pi, %pi),parametric_surface(1+cos(u)+.5*cos(u)*cos(v),.5*sin(v),sin(u)+.5*sin(u)*cos(v),u, -%pi, %pi,v, -%pi, %pi)) $
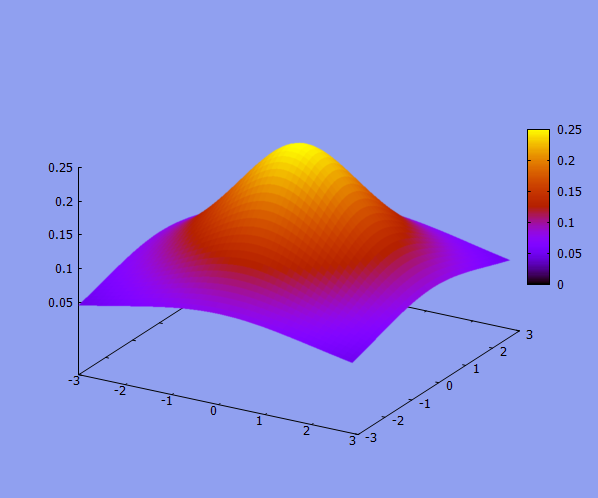
draw3d( enhanced3d=true, explicit(1/(4+x^2+y^2),x,-3,3,y,-3,3) );
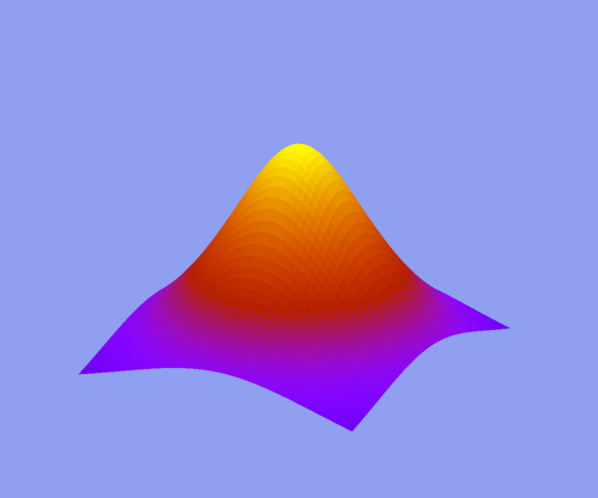
draw3d( enhanced3d=true, axis_3d=false, colorbox=false, explicit(1/(4+x^2+y^2),x,-3,3,y,-3,3) );
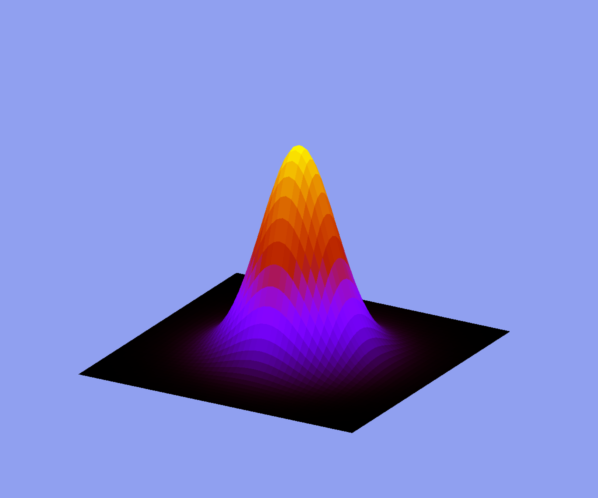
draw3d( enhanced3d=true, axis_3d=false, colorbox=false, explicit(20*exp(-x^2-y^2)-10,x,-3,3,y,-3,3) );
|
|
|